Estimating a reasonable size for a tiny speck of gold that basically looks cube-shaped can be described as trying to guess the cube's width. A problem arises when having that guessed dimension raised to a power of three when trying to calculate the cube's volume. Another problem arises when the actual shape is nothing like a cube. The resulting volume may be off considerably due to size estimation errors. For this reason, use more than one estimate for bracketing in a likely value for the size of the gold in question. Use a size estimate that is likely smaller than the gold in question and then use one that is likely the correct size. Know that your resulting price estimate will only be as good as the estimate of the object's actual volume. (Please, see the example below).
Above, there was discussion of an error created when not knowing the actual dimensions involved. To better illustrate this issue, let’s briefly examine the 1/10th Troy Ounce coin: The coin has a stated diameter of 16.5 mm, a thickness at its edge of 1.19 mm and a mass of 3.393 grams. It has a mix of copper and silver as the impurities with a ratio of 16 to 9, set at 22 karat.
By using the formula for finding the volume of a cylinder, we can produce a reasonable estimate for a volume: radius squared, multiplied by pi, then multiplied by the edge thickness.
Using the basic raw dimensions of the coin to develop a volume mathematically, we generate a volume of 254.45 cubic millimeters. Loading 254.45 cu mm into the QuckGoldTally volume input field (Cube Size, far right), while remembering to also load in the 22 karat and switch the impurity to 16:9(Cu,Ag), we get an expected mass of 4.515 grams. Yet, the stated value for the mass of the coin, given above, is 3.393 grams. How can this be? This difference is due to the fact that the dimensions for the coin are based upon a perfect cylindrical shape. But, an actual coin has pits and indents, making its shape smaller – even though the differences in size seem trivial.
Here we see the perfect cylindrical shape of the idealized coin:
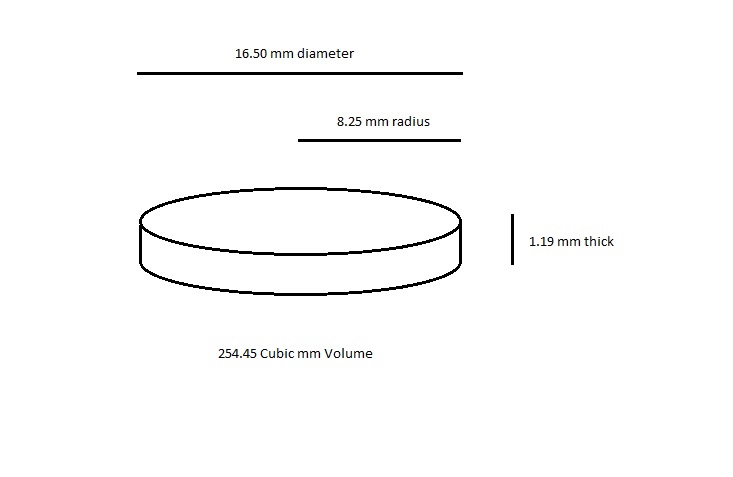
And, here is a view of the actual coin itself, sharing the same outside measurements as the idealized coin, but also having relief detail:

Notice the small differences in thickness along the above coin's face. Though these differences seem trivial, they can produce a significant amount of error when trying to calculate volume. In other words, we don't so much need the general thickness of the coin, measured by a set of calipers, but, rather, the true "average" thickness, taking into account the relief involved.
This next set of images show the actual volume of the coin itself as a cube (below left), the cubic volume of the removed relief detail (below middle) and the idealized cubic volume of the coin, (again, shown as a cube, calculated from coin’s raw, outside dimensions obtained with a set of calipers, seen below right):
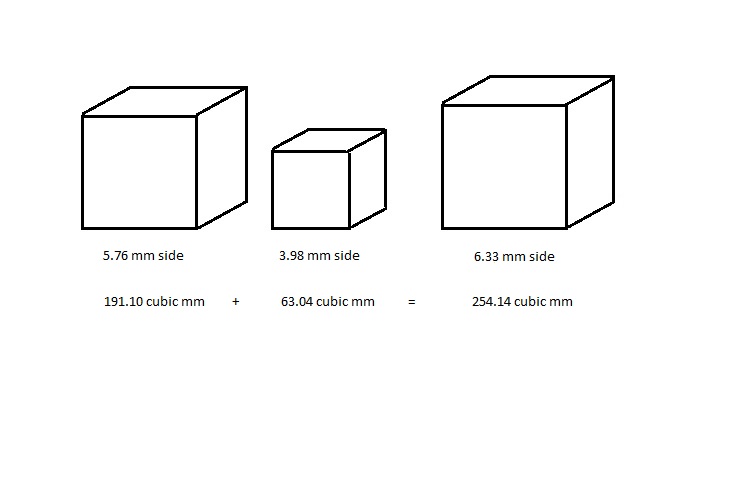
Above, notice how similar the cube on the far left appears with regard to the cube on the far right. Yet, they both differ by the amount equal to the size of the cube in the middle. This goes to show the sort of error involved if relying entirely upon an estimated size in order to glean the likely weight of the object in question. For this reason, use more than one estimate to bracket in a more likely value.